こんにちは。
整形外科医師ブロガーのボククボです。
MATLABの分類学習器アプリで機械学習を始めました。
クリックすれば、分類モデルができちゃう
スグレモノなんですが、
アルゴリズムがわからないと怖いですよね。
まずは、機械学習の基本的な学習アルゴリズムである、
ナイーブ(単純)ベイズ分類器について、
人に説明できる程度に勉強しました。
いろんなサイトを見て勉強したのですが、
数式の添え字が多すぎて、理解するのが大変でした。。。
最初に数式があると、すっきりまとまってよいのですが、
何度も読み直して意味をかみ砕かないといけません。
というわけで、
前半は数式をなるべく使わず、
【前から順番に読んでいくと理解できる】
というのを目標に説明していきます。
目次
分類器とは?
教師あり機械学習において、
分類器/分類モデルとはなんでしょうか。
訓練データには、
着目する特徴量と正解の分類情報が含まれます。
これらのデータから、
アルゴリズムに従って分類モデルを作り、
未知の特徴量データが与えられたときに、
分類クラスを予測できるようにするというものです。
この予測の正答率を上げるために、
分類モデルの作り方がいくつもあり、
それぞれ名前がついています。
今回はそのうちの一つ、
ナイーブ(単純)ベイズ分類器の解説です。
ベイズ分類器とは?
事後確率の概念を用いる分類アルゴリズムです。
高校数学でもやるように、
事後確率の計算には下のベイズの定理が用いられます。
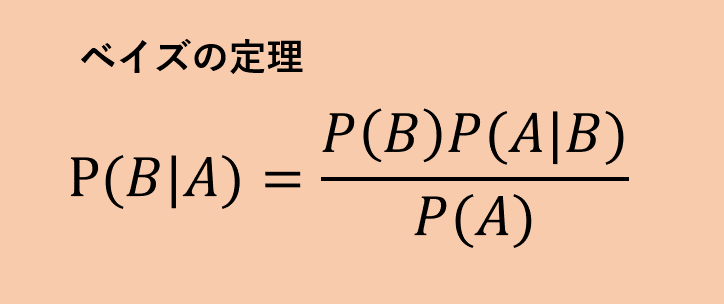
しかし、ベイズ分類器をざっくり理解するのに、
ベイズの定理による計算が必要なわけではありません。
っていうか常人には計算できません。
まず最初に理解すべきことは、ベイズ分類器は
【テスト用特徴量データが与えられたとき、クラスC1に分類される確率】
【テスト用特徴量データが与えられたとき、クラスC2に分類される確率】
という二つの事後確率を比べて分類するということです。
(わかりやすいようにクラスが二つだけの場合に限定して話します。)
いまいち、ピンとこないと思うので、
事後確率と分類の関係を
パチンコを例にして説明してみます。
事後確率
事後確率については、
以前、パチンコを例にして解説しました。
【激アツリーチが来た後、大当たりする確率】は
リーチが来たことが確定していれば、事後確率です。
つまり、平場で大当たりを待っているより、
確率が高い’激アツ’状態です。
この、激アツ状態の確率が事後確率です。
この事後確率は、
試行をたくさん行うことにより簡単に求められます。
(リーチ演出後の大当たりの割合を求めればよい)
パチンコ雑誌では、「演出信頼度」という形で
情報提供されています。
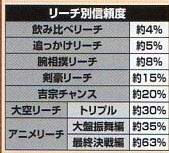
分類への応用
訓練データにより、十分なリーチに関する確率情報があれば、
演出信頼度=事後確率が求まります。
つまり、ある特徴量(リーチの種類)が確定したとき、
各クラス(当たり/ハズレ)になる確率は、下のように表現できます。
【激アツリーチが来たから、当たり確率90%】
【激アツリーチが来たから、ハズレ確率10%】
このような二つの事後確率を分類に利用しようというのが
ベイズ分類器です。
ここでは、
特徴量データ=’激アツリーチ’のとき、’当たり’になる確率が高いので
’当たり’に分類するのです。
このように、特徴量決定時の事後確率が高い方にクラス分類
していくことで、性能のよい分類器を作ろうとするアルゴリズムなのです。
特徴量が1つで連続値の場合
パチンコの例では、
特徴量が1つで、リーチの種類という
離散的な(カテゴリ的な)値を扱いました。
特徴量が離散的であれば、事後確率は、
事象のカウントによって、簡単に計算できます。
特徴量が1つで連続値の場合はどうでしょうか?
こうなると、直接事後確率を推計することはできなくなり、
’確率分布’で考えることが必要になります。
というわけで、すみませんが、そろそろ数式を使います。
分類時に使用する特徴量をXとします。
訓練用データとして、
特徴量:X=x1,x2,...,xn とそれに対応する
分類クラス:C=C1,C2,C1,...,C1,C2
が与えられています。
(簡単のため、分類クラスはC1/C2の2種類としました。)
Xには特徴量として、
単なる連続的な数字(小数とか)が入っていると考えてください。
テスト用(予測したい)データの特徴量がX=aだったとき,
ベイズ分類するために
【C=C1となる事後確率】 P(C=C1|X=a)
【C=C2となる事後確率】 P(C=C2|X=a)
という二つの確率の大小関係を求めたいです。
ここでベイズの定理を利用すると、それぞれ
P(C=C1|X=a)=P(C=C1)×P(X=a|C=C1)/P(X=a)
P(C=C2|X=a)=P(C=C2)×P(X=a|C=C2)/P(X=a)
となります。
どちらもP(X=a)で割っていますが、大小関係を求めるなら
この項は計算する必要はありません。
残りの項を訓練データから推測していきます。
最初の項は、C1,C2に分類される確率なので、
それぞれ
P(C=C1)=C1の個数/訓練データ数
P(C=C2)=C2の個数/訓練データ数
で求められます。(推測してるっていうのが正しいか。)
問題は、分子の2番目の項
P(X=a|C=C1)とP(X=a|C=C2)の計算です。
P(X=a|C=C1)はC1に分類されたことが確定したデータにおいて、
特徴量Xがaとなる確率です。
訓練データから推計するには、
C1に分類された訓練データを集め、その特徴量の分布を調べます。
もちろんバラバラなので、X=aになる確率なんてわかりません。
でも、特徴量が正規分布すると仮定したらどうでしょう?
推計に使う訓練データの平均と標準偏差がわかれば、
確率分布が求まります。
そうすると、X=aとなる確率も求まるわけです。
というわけで、P(X=a|C=C1)とP(X=a|C=C2)も計算できました。
あとは、前述の式の大小関係によって
分類結果が決定されます。
実際の計算はMATLABに任せれば十分ですけどね。
ちなみに、正規分布を仮定したから計算できたことは
忘れてはいけません。
正規(ガウス)分布を仮定して計算したベイズ分類器を
ガウス単純ベイズ分類器と呼びます。
ベルヌーイ分布、多項分布を仮定することもあります。
特徴量が2つの場合を理解する
特徴量が2つの場合はどうなるでしょうか。
特徴量Xは2次元のベクトルになります。
X=(x1,x2)といったイメージです。
(計算には使いませんが)
テストデータもX=(a1,a2) と表記することにします。
P(X=(a1,a2)|C=C1)とP(X=(a1,a2)|C=C2)の計算ができれば、
【C=C1となる事後確率】 P(C=C1|X=(a1,a2))
【C=C2となる事後確率】 P(C=C2|X=(a1,a2))
の大小関係がわかることまでは共通です。
特徴量が1つのときと同様に、
訓練データでC1に分類されたデータの、特徴量Xを集め
確率分布を求めたいのです。
正規分布を仮定することにしても、
2次元ベクトルの正規分布なんて常人には計算できません。
(できなくも無いですが)
そこで、1次元の問題に帰着させることを考えます。
そのために、仮定をもうひとつ加えます。
二つの特徴量が独立に動く
ということです。
二つの特徴量のとる確率が、互いに影響しないのであれば、
積の法則が使えるので、
P(C=C1|X=a1,a2)=P(C=C1|X=a1)×P(C=C1|X=a2)
が成り立ちます。
右辺の2項は特徴量が1つのときと同様に、
正規分布を仮定すれば、計算可能です。
2次元の計算を1次元の計算に単純化するので
’単純’ベイズ分類器
あるいは
’ナイーブ’ベイズ分類器
と呼ばれるわけです。
特徴量がn個の場合を理解する
2次元が理解できればn次元も同じです。
特徴量X=(a1,a2,.....an)のときの計算ですから
P(C=C1|X=a1,a2,..,an)=
P(C=C1|X=a1)×P(C=C1|X=a2)×...×P(C=C1|X=an)
と計算できます。
計算自体はそれほど複雑にはなっておらず’単純’ですね。
まあ、実際の計算はMATLABにお任せですが。
本当に独立なのか?
各特徴量が独立って仮定してもよいものでしょうか?
特徴量がなんの相関もなく完全に独立って、
なかなかないと思います。
独立でなかった場合、どうなるか。
分類精度が下がってしまう可能性があります。
逆にいえば、
結果的に分類精度が良好であるなら、
特徴量が独立でなくても気にしなくてよいとも言えます。
(実際そういうことも多い。)
まとめ
- ベイズ分類器が事後確率を利用した分類法であること
- 特徴量が連続量であれば、分布を仮定する必要があること
- 2つ以上の特徴量だと、互いの独立性を仮定して計算すること
が理解できれば
’ガウス’+’単純’+’ベイズ分類器’
の意味がよくわかると思います。
間違いなどあれば、コメントもしくはTwitterで教えてください。
よろしくお願いします。
