こんにちは。
整形外科医師ブロガーのボククボです。
今回は、数学のお話です。
ベイズの定理とは、事後確率を求める公式ですが、
機械学習による分類モデルにも応用されます。
単純ベイズ分類器について理解するには、
ベイズの定理をがっちり理解することが重要です。
というわけで、誰にでも?わかるように
パチンコを例に解説しようと思います。
- パチンコばっかりやって試験に落ちそうな大学生
- 学校の授業で事後確率が理解できなかった高校生
- 機械学習について勉強中だけど全然わからん
などの方に読んでいただけると幸いです。
目次
事後確率とは?

事後確率なんて言うと、生活に不要な概念に思えますが、
パチンコで例えると
【激熱リーチが来た後で、大当たりする確率】
です。
激熱リーチが来てるんだから、平場より
大当たりしてる確率も跳ね上がってるだろ!
と思いますよね。
その跳ね上がった確率のことです。
パチスロ雑誌では、演出信頼度と書いてあります。
ちなみに
【激熱リーチ】というのを数学的に表現すると、
- 大当たり時に高確率で出現する
- ハズレ時に低確率で出現する
リーチ演出という定義になります。
上の二つの事象は、合わせても低確率になりますので
激レアリーチ=激熱リーチ
ということになります。
(まあ、理論上はハズレ時にのみ
稀にでるリーチってのもありうるのですが。。)
補足:実はリーチ演出の方が後ですが
一応パチンコ台の抽選方法に関する補足です。
混乱する方は読み飛ばしていただいてかまいません。
パチンコは、
ヘソに玉が入った瞬間に大当たりかどうか
決定しています。
激熱リーチ演出を目にするのは、
大当たり抽選が済んでいる後ですが、
便宜上、リーチ後に大当たりが
出現しているものとして考えます。
事後(リーチ後)の大当たり確率を事後確率と呼ぶことにします。
ベイズの定理
A=激熱リーチ(全回転リーチとでもしますか)
B=大当たり
と名付けると
【全回転リーチが来た後で大当たりする確率】
(事後確率)は
P(B❘A) と表します。
P(B|A)=P(A∧B)/P(A)で計算されますが、
(後述します。)
ベイズの定理は少し分子のP(A∧B)を分解します。
*P(A∧B)は、AとBが同時に起きる確率です。
すなわち、
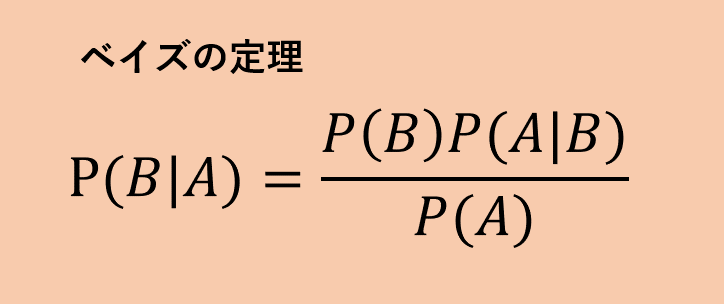
となります。
事後確率は、
P(B)、P(A|B)、P(A)が計算できれば求まるという
公式です。
わけがわからないと思いますので、一つ一つ
パチンコで説明します。
全体の式の意味

分子
繰り返しますが、
分子に記載してあるP(B)P(A|B)というのは
P(A∧B)を分解した形です。
ベイズの定理は、
P(B❘A)=P(A∧B)/P(A)
とも書き直せるわけです。
P(A∧B)というのは、
事後とか事前とか関係なく、
大当たりして、全回転リーチも出る確率です。
なんの演出も出ていない平場で
「全回転リーチがでて大当たりしないかな。。」
なんてボヤキながら待っている確率ですね。
(たぶん1/3000ぐらいでしょうか。)
かなり低い確率になります。
分母
分母はP(A)です。
全回転リーチが出る確率のことです。
P(A)が低い(=レア演出)なほど
事後確率(信頼度)は跳ね上がります。
なぜ、P(A)で割るのかについては、下図を参照ください。
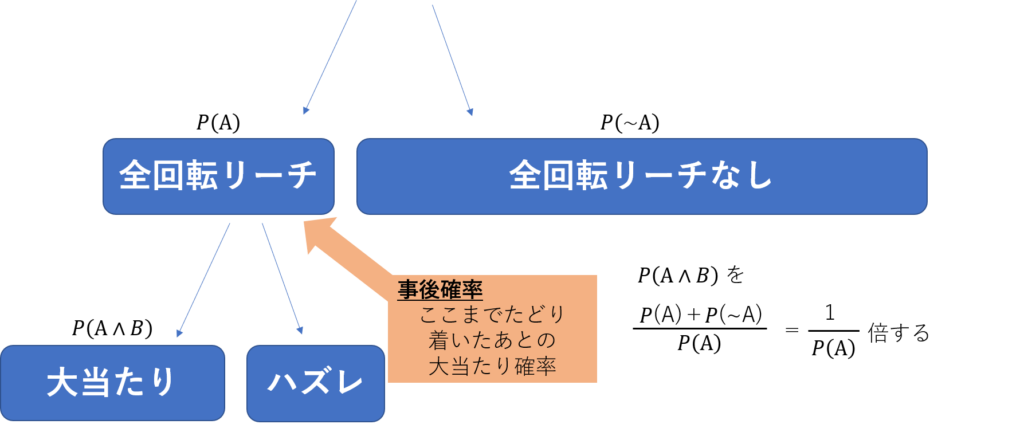
全回転リーチが来てる時点で、かなり
考慮すべき事象が限定されている(P(A)倍になっている)
わけですね。
全回転リーチ以外を介する出来事(あたり、はずれ)
を無視できる。
といってもいいです。
全回転リーチが確定すると、
起こりうる出来事(全事象)が、
P(A)倍とガクンとへるので、
確率が1/P(A)倍になるのです。
P(B)P(A|B)について
ベイズの定理の形に直した場合の
各項の意味について解説します。
P(B)
これは単純に、大当たりの確率ですね。
事前確率と呼ばれるものです。
【エヴァンゲリオン13 超暴走】でいえば
初当たり確率の1/199のことです。
何も事(リーチ演出)が
起こってない状態(事前)での確率ですね。
P(A❘B)
すべての大当たりのうち
全回転リーチを介して大当たりする割合です。
多分数十分の1ぐらいでしょうか。
P(B):大当たり確率
P(B|A):大当たりのうち、全回転リーチを介する割合
なので
P(A∧B)=P(B)×P(A|B)
となることは、理解できます。
尤度
P(A❘B)は尤度(ゆうど)とも呼ばれます。
「尤もらしい(もっともらしい)」の「尤」ですね。
事後確率を考える上では、ピンときませんが、
機械学習でベイズ分類器を理解するのには重要な概念です。
パチンコで例えると、
ホールで大当たりをしている人がいたしたとして、
「全回転リーチを介して当たったんだな」
と推測することが、どれぐらい尤もらしい(ありうるの)か。
というのが尤度です。
つまりは、
すべての大当たりのうち
全回転リーチを介して大当たりする割合ですね。
機械学習では、尤度が定数で与えられることはなく
訓練データから推測される確率分布(関数)の形で表現されます。
この分布は尤度関数と呼ばれ、
単純ベイズ分類器では、
これにテストデータを入れることで
分類クラスをが推定できます。
(また別の記事で解説するかも。)
まとめ
ベイズの定理・事後確率の解説を、
パチンコを題材に解説してみました。
一部の方にとっては、理解しやすいのではないかと
思いましたが、いかがだったでしょうか。
ご意見などあれば、コメントにお願いします。
